T2* Mapping - Multi-echo FLASH#

\(T2^*\) mapping with a multi-echo FLASH sequence.

Imports#

import tempfile
from pathlib import Path

import matplotlib.pyplot as plt
import MRzeroCore as mr0
import numpy as np
import torch
from cmap import Colormap
from einops import rearrange
from mrpro.algorithms.reconstruction import IterativeSENSEReconstruction
from mrpro.data import CsmData
from mrpro.data import KData
from mrpro.data import SpatialDimension
from mrpro.data.acq_filters import is_coil_calibration_acquisition
from mrpro.data.traj_calculators import KTrajectoryIsmrmrd
from mrpro.operators import DictionaryMatchOp
from mrpro.operators.models import MonoExponentialDecay
from mrpro.phantoms.coils import birdcage_2d

from mrseq.scripts.t2star_multi_echo_flash import main as create_seq
from mrseq.utils import combine_ismrmrd_files
from mrseq.utils import sys_defaults

Settings#

We are going to use a numerical phantom with a matrix size of 128 x 128. To ensure we really acquire all radial lines in the steaady state, we use a large number of dummy excitations before the actual image acquisition.

image_matrix_size = [128, 128]

tmp = tempfile.TemporaryDirectory()
fname_mrd = Path(tmp.name) / 't2star.mrd'

Create the digital phantom#

We use the standard Brainweb phantom from MRzero, but we choose the B0- and B1-field to be constant everywhere.

im_dims = SpatialDimension(z=1, y=image_matrix_size[1], x=image_matrix_size[0])
coil_maps = birdcage_2d(6, image_dimensions=im_dims, relative_radius=0.8)

phantom = mr0.util.load_phantom(image_matrix_size)
phantom.B1[:] = 1.0
phantom.B0[:] = 0.0
phantom.coil_sens = rearrange(coil_maps[0, ...], 'coils z y x -> coils x y z')

Create the \(T2^*\) mapping sequence#

To create the \(T2^*\) multi-echo FLASH sequence, we use the previously imported \(T2^*\) multi-echo FLASH.

sequence, fname_seq = create_seq(
    system=sys_defaults,
    test_report=False,
    timing_check=False,
    fov_xy=float(phantom.size.numpy()[0]),
    n_readout=image_matrix_size[0],
    n_echoes=8,
    n_pe_points_per_cardiac_cycle=8,
    acceleration=2,
)

Current echo time = 2.095 ms
Current repetition time = 23.860 ms
Acquisition window per cardiac cycle = 190.880 ms

Saving sequence file 't2star_multi_echo_flash_200fov_128nx_2us_0-7pe.seq' into folder '/home/runner/work/mrseq/mrseq/examples/output'.
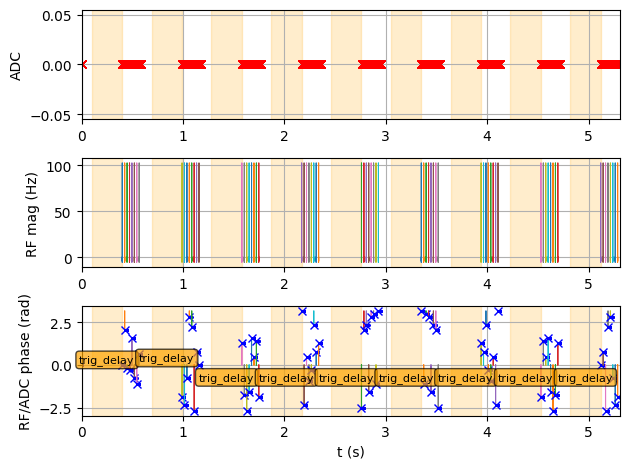
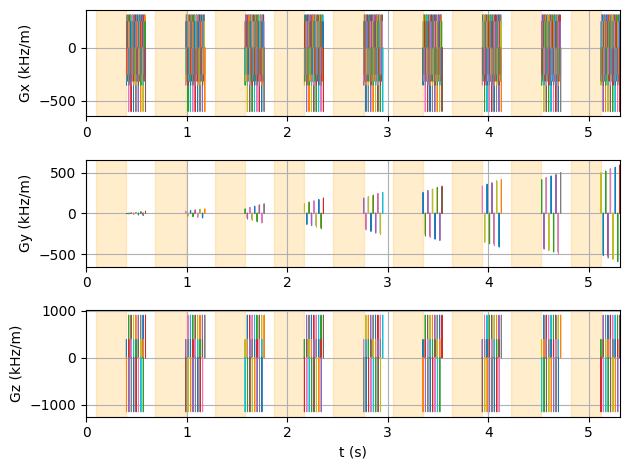
_images/9bc6ee1269204ab8926c0c028a5a5071840eda44496edbbef911e7fd6b37848d.png _images/a051a121a1f62ce4c0c6585bbefbc817bffa5e15ae83584f747548f2c29ab9a6.png

Simulate the sequence#

Now, we pass the sequence and the phantom to the MRzero simulation and save the simulated signal as an (ISMR)MRD file.

mr0_sequence = mr0.Sequence.import_file(str(fname_seq.with_suffix('.seq')))
signal, ktraj_adc = mr0.util.simulate(mr0_sequence, phantom, accuracy=1e-1)
mr0.sig_to_mrd(fname_mrd, signal, sequence)
combine_ismrmrd_files(fname_mrd, Path(f'{fname_seq}_header.h5'))

>>>> Rust - compute_graph(...) >>>
Converting Python -> Rust: 0.001381197 s
Compute Graph
Computing Graph: 0.31376714 s
Analyze Graph
Analyzing Graph: 0.000706598 s
Converting Rust -> Python: 0.0067722 s
<<<< Rust <<<<

<ismrmrd.hdf5.Dataset at 0x7fba30c915e0>

Reconstruct the image#

We use MRpro for the image reconstruction.

kdata = KData.from_file(str(fname_mrd).replace('.mrd', '_with_traj.mrd'), trajectory=KTrajectoryIsmrmrd())

kdata_calib = KData.from_file(
    str(fname_mrd).replace('.mrd', '_with_traj.mrd'),
    trajectory=KTrajectoryIsmrmrd(),
    acquisition_filter_criterion=is_coil_calibration_acquisition,
)
csm = CsmData.from_kdata_inati(kdata_calib[0], downsampled_size=64, smoothing_width=9)
recon = IterativeSENSEReconstruction(kdata, csm=csm, n_iterations=8)
idata = recon(kdata)

/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/mrpro/data/KData.py:166: UserWarning: No vendor information found. Assuming Siemens time stamp format.
  warnings.warn('No vendor information found. Assuming Siemens time stamp format.', stacklevel=1)

We can now visualize the images obtained at the different echo times.

idat = idata.rss().abs().numpy().squeeze()
fig, ax = plt.subplots(1, idat.shape[0], figsize=(3 * idata.shape[0], 3))
for i in range(idat.shape[0]):
    ax[i].imshow(idat[i, :, :], cmap='gray')
    ax[i].set_title(f'TE = {int(idata.header.te[i] * 1000)} ms')
    ax[i].set_xticks([])
    ax[i].set_yticks([])
_images/30149cbbc25c32848fec41a0755dfa6d08de0ce39b823f1ffad0eef9233eeb34.png

Estimate \(T2^*\)#

We use a dictionary matching approach to estimate the \(T2^*\) maps. Afterward, we compare them to the input and ensure they match but first, we need to calculate \(T2^*\) using \(1/T2^* = 1/T2 + 1/T2'\).

t2star = 1 / (1 / phantom.T2 + 1 / phantom.T2dash)

dictionary = DictionaryMatchOp(MonoExponentialDecay(decay_time=idata.header.te), index_of_scaling_parameter=0)
dictionary.append(torch.tensor(1.0), torch.linspace(0.01, 0.8, 1000)[None, :])
m0_match, t2star_match = dictionary(idata.data[:, 0, 0])

t2star_input = np.roll(rearrange(t2star.numpy().squeeze()[::-1, ::-1], 'x y -> y x'), shift=(1, 1), axis=(0, 1))
obj_mask = np.zeros_like(t2star_input)
obj_mask[t2star_input > 0] = 1
t2star_measured = t2star_match.numpy().squeeze() * obj_mask

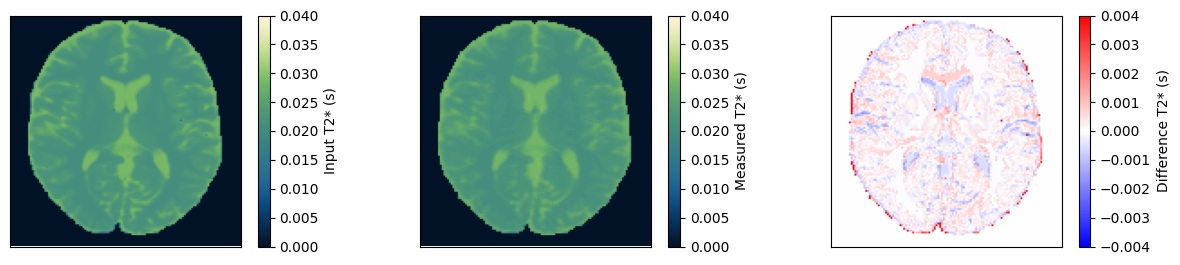
fig, ax = plt.subplots(1, 3, figsize=(15, 3))
for cax in ax:
    cax.set_xticks([])
    cax.set_yticks([])

im = ax[0].imshow(t2star_input, vmin=0, vmax=0.04, cmap=Colormap('navia').to_mpl())
fig.colorbar(im, ax=ax[0], label='Input T2* (s)')

im = ax[1].imshow(t2star_measured, vmin=0, vmax=0.04, cmap=Colormap('navia').to_mpl())
fig.colorbar(im, ax=ax[1], label='Measured T2* (s)')

im = ax[2].imshow(t2star_measured - t2star_input, vmin=-0.004, vmax=0.004, cmap='bwr')
fig.colorbar(im, ax=ax[2], label='Difference T2* (s)')

relative_error = np.sum(np.abs(t2star_input - t2star_measured)) / np.sum(np.abs(t2star_input))
print(f'Relative error {relative_error}')
assert relative_error < 0.02

Relative error 0.017385253682732582
_images/da571f883361981a32019bb0ed6bae35ae21fe5423330c5c1070e145cecfc6c1.png
Show Source